LeetCode Link: 863. All Nodes Distance K in Binary Tree
Language: C#
Problem Statement
Given the root of a binary tree, the value of a target node target, and an integer k, return an array of the values of all nodes that have a distance k from the target node.
You can return the answer in any order.
Examples
Example 1:
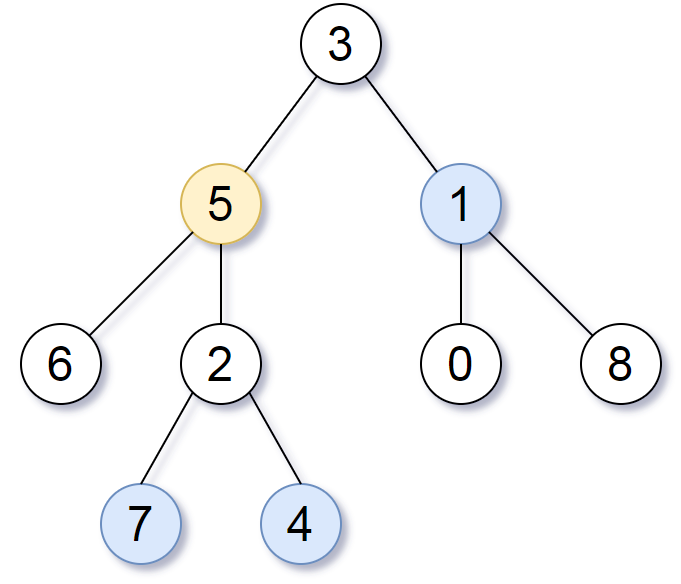 Input: root = [3,5,1,6,2,0,8,null,null,7,4], target = 5, k = 2
Input: root = [3,5,1,6,2,0,8,null,null,7,4], target = 5, k = 2
Output: [7,4,1]
Explanation: The nodes that are a distance 2 from the target node (with value 5) have values 7, 4, and 1.
Example 2:
Input: root = [1], target = 1, k = 3
Output: []
Constraints
- The number of nodes in the tree is in the range [1, 500].
- 0 <= Node.val <= 500
- All the values Node.val are unique.
- target is the value of one of the nodes in the tree.
- 0 <= k <= 1000
Solution
/**
* Definition for a binary tree node.
* public class TreeNode {
* public int val;
* public TreeNode left;
* public TreeNode right;
* public TreeNode(int x) { val = x; }
* }
*/
Approach 1
public class Solution
{
private Dictionary<TreeNode, TreeNode> parentMap = new();
private HashSet<TreeNode> visited = new();
public IList<int> DistanceK(TreeNode root, TreeNode target, int k)
{
ConstructParentMap(root, null);
return Traverse(target, k);
}
private List<int> Traverse(TreeNode root, int k)
{
var q = new Queue<TreeNode>();
q.Enqueue(root);
int dist=0;
while (q.Count > 0)
{
var list = new List<TreeNode>();
var resp = new List<int>();
while (q.Count > 0)
{
var item = q.Dequeue();
visited.Add(item);
resp.Add(item.val);
list.Add(item);
}
if (dist == k)
{
return resp;
}
foreach(var item in list)
{
if (item.left != null && !visited.Contains(item.left))
{
q.Enqueue(item.left);
}
if (item.right != null && !visited.Contains(item.right))
{
q.Enqueue(item.right);
}
if (parentMap[item] != null && !visited.Contains(parentMap[item]))
{
q.Enqueue(parentMap[item]);
}
}
dist++;
}
return new List<int>();
}
private void ConstructParentMap(TreeNode root, TreeNode parent)
{
if (root is null)
{
return;
}
parentMap[root] = parent;
ConstructParentMap(root.left, root);
ConstructParentMap(root.right, root);
}
}
Approach 2: Recurssion
/**
* Definition for a binary tree node.
* public class TreeNode {
* public int val;
* public TreeNode left;
* public TreeNode right;
* public TreeNode(int x) { val = x; }
* }
*/
public class Solution {
private Dictionary<TreeNode, TreeNode> parentMap = new();
private HashSet<TreeNode> visited = new();
public IList<int> DistanceK(TreeNode root, TreeNode target, int k) {
ConstructParentMap(root, null);
var list = new List<int>();
Traverse(target, list, 0, k);
return list;
}
private void Traverse(TreeNode root, List<int> list, int k, int target)
{
if (root is null)
{
return;
}
if (visited.Contains(root))
{
return;
}
visited.Add(root);
if (k == target)
{
list.Add(root.val);
return;
}
Traverse(root.left, list, k + 1, target);
Traverse(root.right, list, k + 1, target);
Traverse(parentMap[root], list, k + 1, target);
}
private void ConstructParentMap(TreeNode root, TreeNode parent)
{
if (root is null)
{
return;
}
parentMap[root] = parent;
ConstructParentMap(root.left, root);
ConstructParentMap(root.right, root);
}
}
Complexity
Time Complexity: O(N)
Space Complexity: O(N)